
Winston Campeau
Ph.D. Candidate
| Email: | winston.campeau@carleton.ca |
| Office: | Office: 4440C CTTC Lab: 227 Nesbitt Building |
Research Project:
An investigation of scale-free and self-similar phenomena as a general feature of evolution.
Research Interests:
Anything in the set containing the intersection of computer science, mathematics, statistics, and biology. I have recently been active in the evolution of optimal searching patterns, but I am currently looking into how 1/f noise – arguably the null case for environmental variation – selects for constraints on adaptation.
Recent Publications:
Campeau W, Simons AM, Stevens B (2023). Intermittent search, not strict Lévy flight, evolves under relaxed foraging distribution constraints. The American Naturalist. DOI: https://doi.org/10.1086/729220 [PDF]
Campeau W, Simons AM, Stevens B (2022). The evolutionary Maintenance of Lévy flight foraging. PLOS: Computational Biology. DOI: https://doi.org/10.1371/journal.pcbi.1009490

(I was a prominent figure at the 2022 Helsinki Summer School on Mathematical Ecology and Evolution)
Side Projects:
The Collatz Conjecture
I have a small obsession with the Collatz Conjecture. Pick any positive, non-zero integer. If that integer is even, divide by 2. Else (otherwise odd), multiple by 3 and add 1. Without fail, as far as we know, you will always end up at 1.
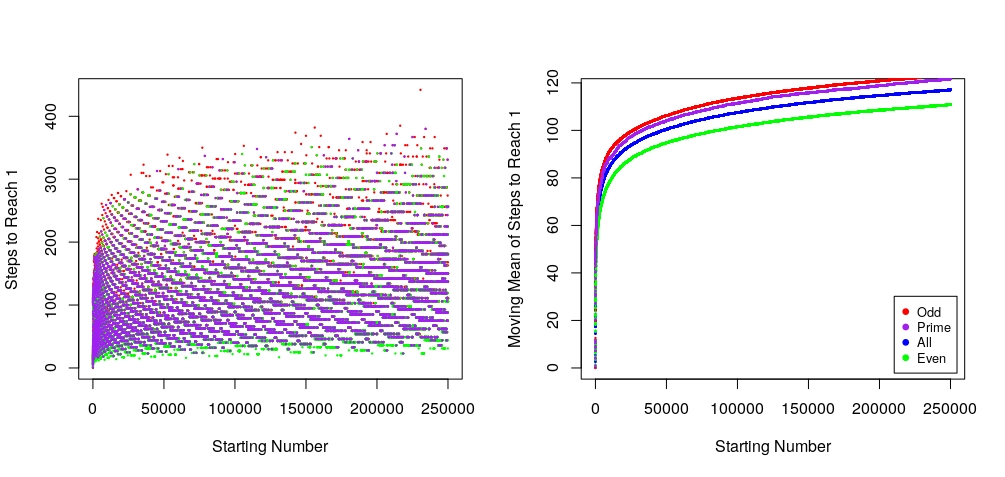
The above figure is a computational approach to the Collatz Conjecture for the integers 1 through 250’000. (Left) Shows the number of steps for each integer to reach 1. (Right) Shows the moving average number of steps for the even, odd, prime, and set of ‘all’ integers (R Code: Here).
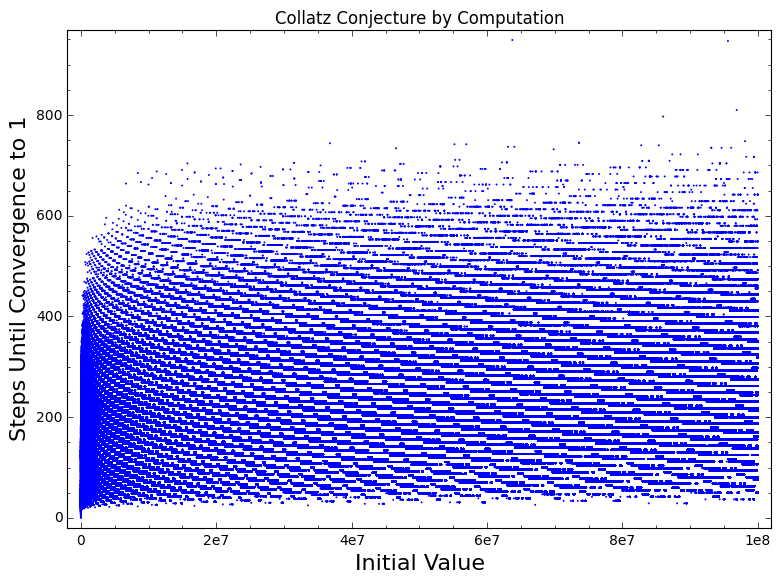
The above figure is the Collatz Conjecture for the integers from 1 to 100’000’000 (Code: Here). NB: This figure was produced in Sage Notebook, but I have provided a method of generating similar plots with the matplot library.
Documents as Noise
Below is the first 10’000 words of the Origin of Species, starting from, and including, the section title “Introduction”. Each word is binned by length, mapped to a colour according to a heat map, and drawn as a pixel. Blues represent shorter words and reds represent longer words. Notice that there are predominantly blues with a speckling of yellow and the rare red pixel. This is something like 1/f noise, which can be observed by the histogram on the right; low magnitude events (short length words) are much more common than high magnitude events (long length words).

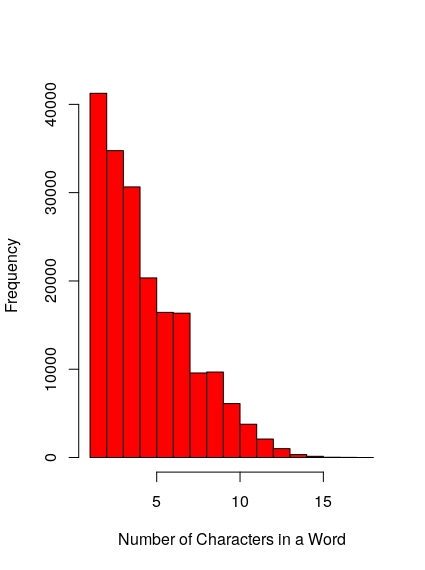
Given the max word length in the Origin of Species is 18, and minimum 1, we can generate similar visualizations of a ‘white noise document’ (below left) and a ‘Brownian document’ (below right).


R gist (very raw code) and formatted copy of Origin of Species available here.