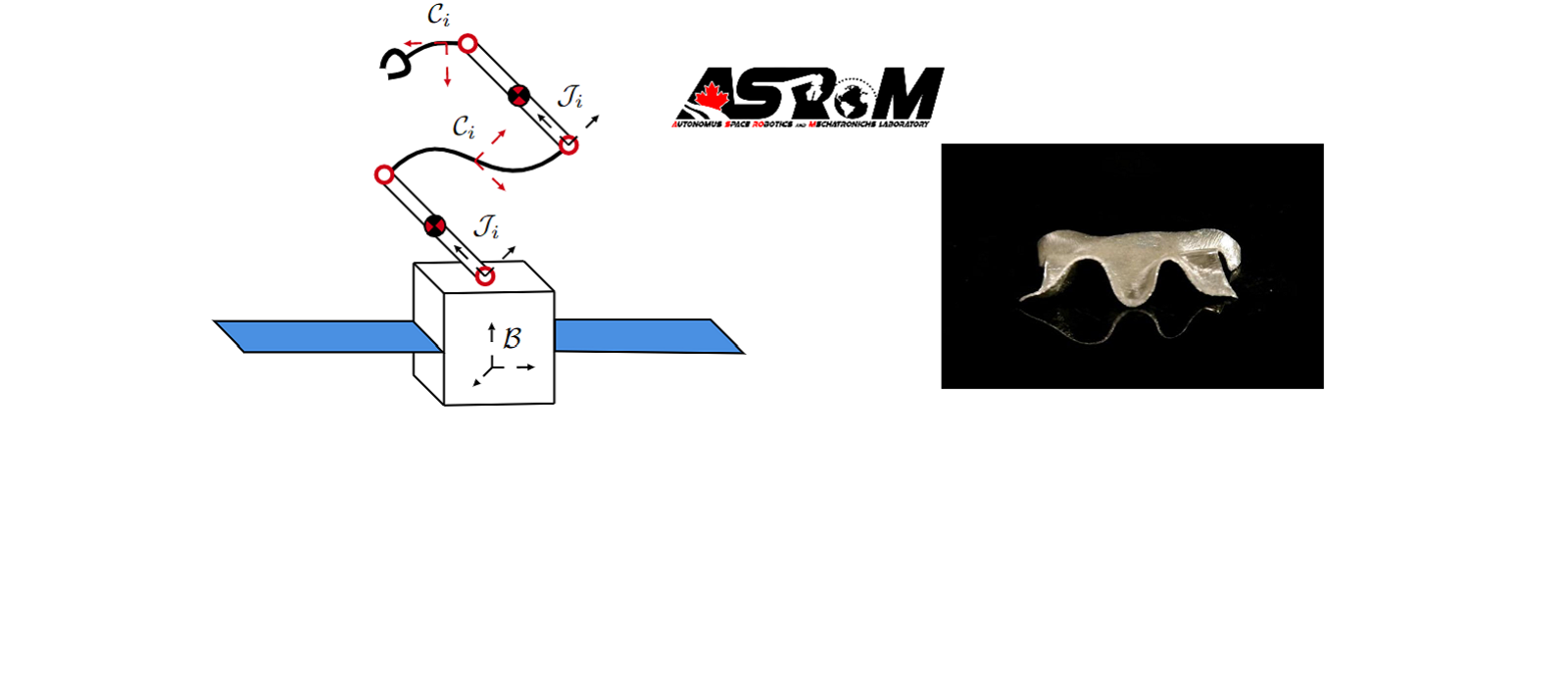
Soft robotic systems offer dexterity, redundancy, and adaptability, crucial in robotic operations in hostile and partially-known environments. They are light, compact, and compliant making them attractive for technology solutions in space applications. Despite their advantages, dynamic modeling and GN&C of soft robots are yet to be significantly advanced to facilitate their commissioning in future terrestrial and space robotic missions. This research seeks to address some of the shortcomings in the modeling and control of soft robots in two main schemes:
- A Lie group-theoretic approach to fast dynamic modeling and output motion/compliance control of soft continuum space manipulators realized as rigid-flexible multi-body systems.
- Geometric modeling of 2-dimensional soft robots made of Cosserat continuum and investigating their shape morphing capabilities for adaptability to environmental changes and mission requirements.
We study the non-linearities due to large finite deformations and material properties of soft robots using a geometric approach to continuum mechanics. The findings of this research are validated and tested in high-fidelity simulation platforms and experimental setups.