The Department of Mechanical and Aerospace Engineering would like to share the good news that one of our Ph.D. students, Zach Copeland, has had his paper, “Multi-modal Continuous Approximate Synthesis of Planar Four-bar Function Generators” accepted for publication in the International Journal of Mechanisms and Robotic Systems. Zach has taken the time to explain to our readers what his paper is about, both in technical terms, and in layman’s terms.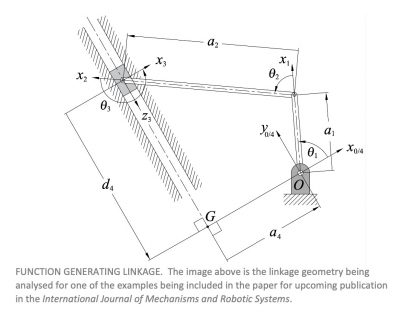
For our technical readers out there, Zach’s paper introduces a novel multi-modal continuous approximate synthesis algorithm for planar four-bar function generators. The synthesis equation is the sum of the squared algebraic input-output (IO) equations integrated over the different prescribed input variable parameter ranges. These equations have been developed by Professor M. John D. Hayes, Ph.D., P.Eng., Department of Mechanical and Aerospace Engineering at Carleton University, and fellow Carleton University Ph.D. student, Mirja Rotzoll.
Every planar four-bar mechanism explicitly generates six distinct functions, each uniquely determined by one set of link parameter constants. These six functions relate some input parameter, typically an angle, and a corresponding output angle. For example, changing the angle of the first link in a 4R linkage, and how this input angle change alters the angle of the final bar within a linkage, which is referred to as the input-output function.
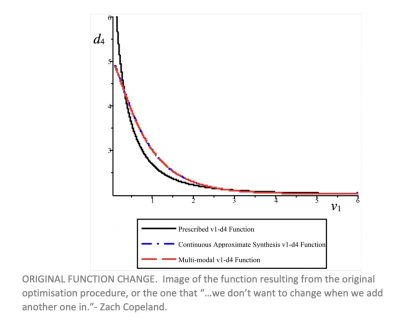
This paper examines the simultaneous continuous approximate synthesis of two related perturbed, but not competing functions between different pairs of joint variables that, in general, require different link constants to generate. However, some small alteration to the relationship between your input link and an intermediate joint angle may be desired in order to improve a process in some way. Previous methods of function generator synthesis have no way of accounting for the joint angles of intermediate links during the design process, but only after a final design has been achieved.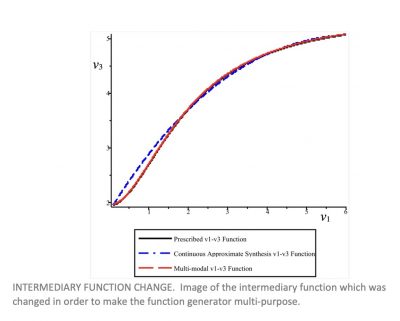
The optimisation presented in this paper involves identifying the best compromise link lengths in order to maintain some given input-output relationship, while altering the relationship between the input angle and an intermediary joint angle. Planar 4R and RRRP examples are presented where two different functions, one primary and the other perturbed secondary, are generated over continuous ranges between the specified input variable parameter and the associated output variable parameter.
In Layman’s terms, Zach has explained that it is quite common in industrial applications to design a rudimentary mechanical system which performs a given task, which is often referred to as designing a function generator. Four-bar linkages, which can be used to relate some change of input to a desired output result have been employed for over 100 years to accomplish this. Through the emergence of more advanced geometric modelling techniques for designing these four-bar linkages in recent years, the question was asked about whether or not we could design a four-bar linkage to generate two separate functions, or tasks, at the same time, but in different joints. This means that multiple processes or functions could be run from a single linkage, simultaneously.
This paper explores this exact problem; it is shown that when given a linkage which produces an original input-output relationship, we can modify the intermediate joint functions slightly, without fundamentally changing the original function which was generated. The algorithm operates by finding the best compromise of link lengths to satisfy both problems, thus allowing the four-bar linkage to simultaneously perform two tasks.
The Department of Mechanical and Aerospace Engineering is very proud of Zach and what he has achieved. You can expect to be able to read Zach’s paper in the upcoming few months in the International Journal of Mechanisms and Robotic Systems, so keep an eye out for it.
Ph.D. candidate, Zach Copeland is a student of Dr. M. John D. Hayes of the Department of Mechanical and Aerospace Engineering at Carleton University.
Friday, December 2, 2022
Department of Mechanical and Aerospace Engineering
Carleton University
Ottawa, Ontario



